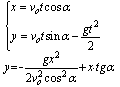Kinematyka- wzory, prawa
Układ odniesienia. Pojęcie ruchu
Układ odniesienia jest to układ współrzędnych związany z ciałem lub zespołem ciał względem, których obserwujemy zmianę położenia jakiegokolwiek ciała. Rozróżniamy układ odniesienia:- jednowymiarowy
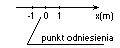
- dwuwymiarowy
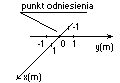
- trójwymiarowy
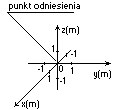
Ruch
Przez ruch ciała rozumiemy zmianę jego położenia względem innych ciał (układu odniesienia)Względność
Względność ruchu polega na tym, iż dane ciało może być w stanie spoczynku względem jednego układu odniesienia, zaś względem innego może znajdować się w ruchuPołożenie i przemieszczenie
Wektor położenia
Wektor położenia, jest to wektor łączący początek układu z punktem, w którym w danej chwili przebywa ciało.Wektor przemieszczenia
Wektor przemieszczenia (przemieszczenie), jest to różnica między kolejnymi wektorami położeń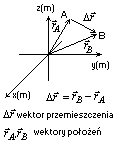
Zobacz symulację wektora położenia i przemieszczenia
WEKTOR POŁOŻENIA I PRZEMIESZCZENIA

Zobacz
Ruch postępowy i obrotowy- definicje
Ruch postępowy
Ciało porusza się ruchem postępowym, jeżeli jego poszczególne punkty zakreślają tory równe i wzajemnie równoległe. Jeżeli tymi torami są linie proste, ruch ciała nazywamy prostoliniowym, gdy są krzywe-krzywoliniowym.Ruch obrotowy
Ruch obrotowy, to taki ruch, w którym wszystkie punkty ciała poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu.Tor ruchu
Tor ruchu, jest to zbiór punktów, w których znajdowało się ciało w kolejnych chwilach ruchu.Pojęcie prędkości
Prędkość
Prędkością w dowolnym ruchu nazywamy stosunek wektora przemieszczenia do czasu, w którym to przemieszczenie nastąpiło.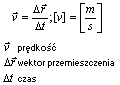
Prędkość chwilowa
Prędkość chwilowa, jest to stosunek przemieszczenia, które nastąpiło w bardzo krótkim czasie, do tego czasu.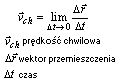
Prędkość średnia
Prędkość średnia, jest to stosunek przemieszczenia do czasu, w którym ono nastąpiło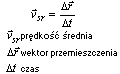
Ruch jednostajny prostoliniowy
Ruch jednostajny prostoliniowy (cechy ruchu)
Stosunek przemieszczenia do czasu, w którym ono nastąpiło jest wielkością stałą- prędkość nie zmienia się podczas trwania ruchu (v = const); torem ruchu jest lina prosta.Równanie ruchu jednostajnego prostoliniowego

Wyprowadzenie równania ruchu jednostajnego prostoliniowego
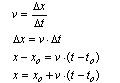
Wykres prędkości w ruchu jednostajnym prostoliniowym
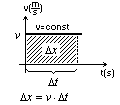
Wartość pola pod wykresem v(t) odpowiada wartości przebytej drogi.
Wykres położenia w ruchu jednostajnym prostoliniowym
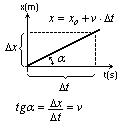
Wartość tangensa kąta nachylenia prostej x(t) odpowiada wartości prędkości
Przyspieszenie. Wektor przyspieszenia
Przyspieszeniem nazywamy stosunek przyrostu prędkości do czasu, w którym ten przyrost nastąpił. Jest to wielkość wektorowa, której kierunek i zwrot jest taki sam jak kierunek i zwrot przyrostu wektora prędkości.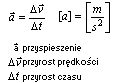
W ruchu prostoliniowym, w którym wartość prędkości wzrasta, wektory przyspieszenia i prędkości są zwrócone zgodnie. W ruchu, w którym wartość prędkości maleje, wektor przyspieszenia jest zwrócony przeciwnie do wektora prędkości.
Ruch jednostajnie przyspieszony
Ruch jednostajnie przyspieszony to ruch, w którym w każdej jednostce czasu szybkość wzrasta o te samą wartość nazywamy ruchem jednostajnie przyspieszonym. Przyspieszenie w tym ruchu jest stałe (a=const) i większe od zera.Szybkość
Szybkość w ruchu jednostajnie przyspieszonym
Położenie w ruchu jednostajnie przyspieszonym
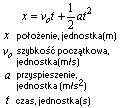
Wykres szybkości od czasu
Wykres szybkości od czasu v(t) w ruchu jednostajnie przyspieszonym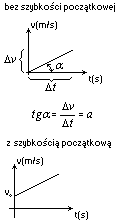
Wartość tangensa kąta nachylenia prostej v(t) odpowiada wartości przyspieszenia. Wartość pola pod wykresem v(t) odpowiada wartości przebytej drogi
Wykres przyspieszenia od czasu
Wykres przyspieszenia od czasu a(t) w ruchu jednostajnie przyspieszonym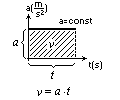
Wartość pola pod wykresem a(t) odpowiada wartości prędkości.
Wykres położenia od czasu
Wykres położenia od czasu x(t) w ruchu jednostajnie przyspieszonym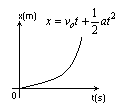
Wyprowadzenie zależności na położenie x(t) w ruchu jednostajnie przyspieszonym
Zakładamy, że ciało posiada już prędkość początkową i porusza się ze stałym przyspieszeniem większym od zera. Przy wyprowadzeniu wzoru skorzystamy z tego, że wartość pola pod wykresem v(t) odpowiada wartości położenia.
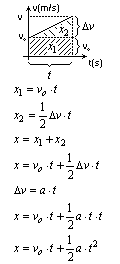
Ruch jednostajnie opóźniony
Ruchem jednostajnie opóźnionym nazywamy taki ruch, w którym wartość prędkości maleje liniowo z czasem. Przyspieszenie jest stałe i mniejsze od zera- czyli jest zwrócone przeciwnie do wektora prędkości.Przyspieszenie w ruchu jednostajnie opóźnionym
Przyspieszenie w ruchu jednostajnie opóźnionym jest stałe i mniejsze od zera. Mniejsze od zera, oznacza, że zwrot tego wektora jest przeciwny do zwrotu wektora prędkości.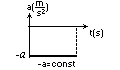
Szybkość w ruchu jednostajnie opóźnionym
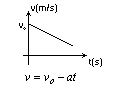
Położenie w ruchu jednostajnie opóźnionym
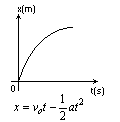
Ruch prostoliniowy niejednostajnie zmienny
Ruch prostoliniowy niejednostajnie zmienny to taki ruch, w którym przyspieszenie nie jest stale w czasie, torem jest linia prosta.Wykres zależności przyspieszenia od czasu a(t)
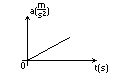
Ciało porusza się coraz to szybciej ze zmiennym przyspieszeniem, jego szybkość rośnie coraz szybciej z każdą chwilą czasu.
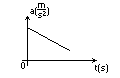
Ciało porusza się coraz to szybciej ze zmiennym przyspieszeniem, jego szybkość rośnie coraz wolniej z każdą chwilą czasu.
Interpretacja ruchu na podstawie wykresu a(t)
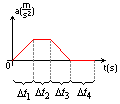
1) W tym przedziale czasu ciało porusza się coraz to szybciej, jego przyspieszenie z każdą chwilą wzrasta.
2) W tym przedziale czasu ciało porusza się ze stałym przyspieszeniem (a=const) większym od zera. Jego prędkość rośnie liniowo- mamy do czynienia z ruchem jednostajnie przyspieszonym
3) W tym przedziale czasu ciało porusza się coraz to szybciej (przyspieszenie jest dodatnie a>0), pomimo że jego przyspieszenie maleje z każdą chwilą
4) W tym przedziale czasu przyspieszenie ciała wynosi zero, szybkość ciała nie ulega zmianie-ciało porusza się ruchem jednostajnym (v=const)
Ruch krzywoliniowy
Przyspieszenie w ruchu krzywoliniowym
Przyspieszenie w ruchu krzywoliniowym występuje zawsze, nawet wtedy, gdy ciało porusza się ze stałą szybkością. W tym wypadku zmienia się kierunek wektora prędkości. Przyrost wektora prędkości (delta)v jest różny od zera, co zgodnie z definicją przyspieszenia jest warunkiem występowania przyspieszenia. Przyspieszenie to nosi nazwę przyspieszenia dośrodkowego.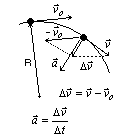
Przyspieszenie dośrodkowe
Przyspieszenie dośrodkowe, jest to przyspieszenie, które zawsze występuje, gdy ciało porusza się po torze krzywoliniowym niezależnie od tego czy wartość prędkości jest stała czy też nie.
Przyspieszenie dośrodkowe jest wielkością wektorową, kierunek wektora przyspieszenia jest równoległy do promienia krzywizny toru a zwrot skierowany jest do środka krzywizny.
Przyspieszenie całkowite w ruchu krzywoliniowym
Jeżeli ciało porusza się po torze krzywoliniowym ze zmianą wartości szybkości to występuje przyspieszenie dośrodkowe i przyspieszenie styczne. Całkowite przyspieszenie jest sumą wektorów tych przyspieszeń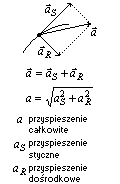
Wyprowadzenie wzoru na wartość przyspieszenia dośrodkowego
Zakładamy, że ciało porusza się ze stałą szybkością po okręgu o promieniu R.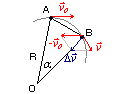
Korzystając z definicji przyspieszenia zapiszemy(zmianę przyrostu wektora prędkości określimy z różnicy wektorów prędkości w punkcie B i A)
Dla małych kątów (α- odległości kątowych) możemy przyjąć, iż długość łuku AB i długość odcinka AB są w przybliżeniu równe.
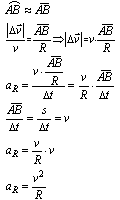
Ruch po okręgu- wielkości opisujące
Okres ruchu jednostajnego po okręgu
Okres ruchu jednostajnego po okręgu jest to czas, w którym ciało zatacza pełny okrąg. Przyjęto go oznaczać symbolem T. Droga przebyta w tym czasie jest równa obwodowi okręgu.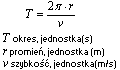
Częstotliwość
Częstotliwość jest to liczba okrążeń wykonanych w jednostce czasu.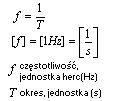
Prędkość kątowa
Prędkość kątowa to stosunek zakreślanego kąta (α)- drogi kątowej do czasu, w którym ten kąt został zakreślony. Wielkość tą wyrażamy w radianch na sekundę (rad/s)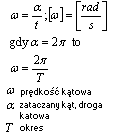
Związek prędkości liniowej z prędkością kątową

Związki przyspieszenia dośrodkowego
Związki przyspieszenia dośrodkowego z prędkością liniową, prędkością kątową, okresem, częstotliwością
Rzut poziomy
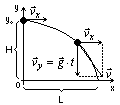
Równanie toru w rzucie poziomym
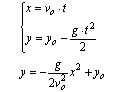
Zasięg rzutu poziomego
Rzut ukośny
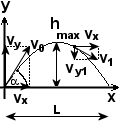
Równanie toru w rzucie ukośnym