Korzystając z przedstawionych na rysunku a0 i b) zależności v(t) oblicz: jak ...

Korzystając z przedstawionych na rysunku a0 i b) zależności v(t) oblicz: jak daleko od punktu startu znajduje się ciało po 5 s; średnia szybkość ciała; narysuj zależność przyspieszenia od czasu.

Rozwiązanie wybranego zadania z fizyki

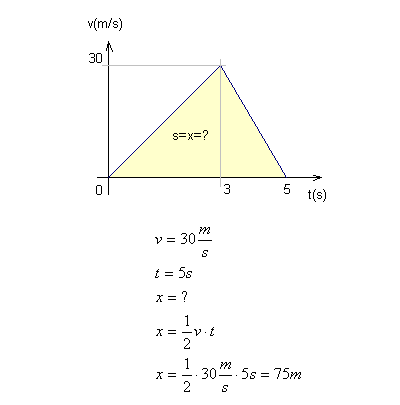
Obliczamy odległość dla przypadku a)- wartość pola pod wykresem v(t) odpowiada odległości ciała od punktu startu. Zauważmy, że pole to trójkąt. Położenie (x) ciała obliczymy przy pomocy wzoru na pole trójkąta, w którym podstawa ma wymiar czasu a wysokość ma wymiar szybkości

Obliczamy średnią szybkość dla przypadku a)

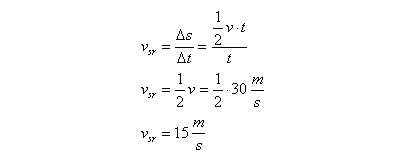
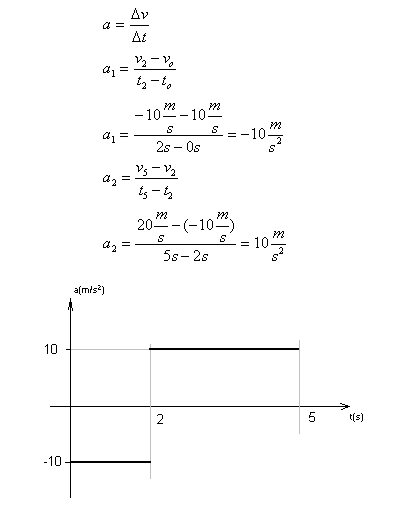
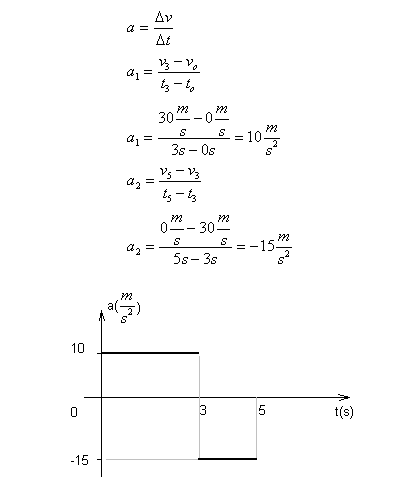
Wykres przyspieszenia od czasu dla przypadku a). Uwaga: ciało od zerowej do trzeciej sekundy poruszało się ruchem jednostajnie przyspieszonym a od trzeciej sekundy do piątej jednostajnie opóźnionym.

Obliczamy odległość dla przypadku b)- wartość pola pod wykresem v(t) odpowiada odległości ciała od punktu startu. Rachunek przeprowadzamy na tych samych zasadach, co dla przykładu a). Dla ułatwienia podzielimy sobie całkowity czas ruchu na trzy przedziały czasowe. Zaznaczymy je na poniższym wykresie i wykonamy odpowiedni rachunek.

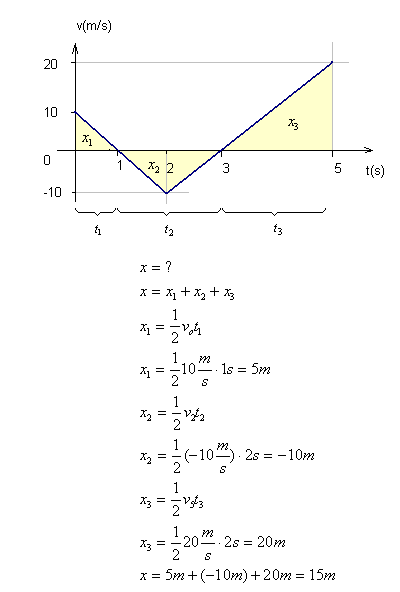
Obliczamy średnią szybkość dla przypadku b) Uwaga: droga ,jaką przebędzie ciało w tym czasie odpowiada sumie modułów (wartości bezwzględnej) położeń.

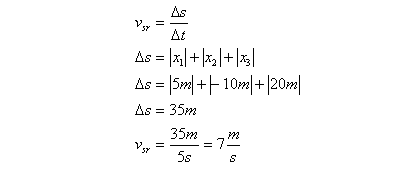
Wykres przyspieszenia od czasu dla przypadku b) Na podstawie podanego wykresy v(t) możemy wywnioskować, że ciało:
- od zerowej do pierwszej sekundy ruchu poruszało się ruchem jednostajnie opóźnionym i przybliżało się do punktu odniesienia.
-od pierwszej sekundy do drugiej ruchem jednostajni przyspieszonym i oddalało się od punktu odniesienia.
-od drugiej sekundy do trzeciej poruszało się ruchem jednostajnie opóźnionym i przybliżało się do punktu odniesienia
-od trzeciej sekundy do piątej poruszało się ruchem jednostajni przyspieszonym i oddalało się od punktu odniesienia.

Ale wartości przyspieszeń są tylko dwie! Proste v(t) nie łamią się w 1 i 3 sekundzie ruchu. Zmiana kąt nachylenia występuje tylko w 2 sekundzie. Stad dla skrócenia rachunku możemy obliczyć tylko dwie wartości przyspieszenia. Będzie to w przedziale od zerowej do drugiej sekundy i od drugiej sekundy do piątej.